人形机器人建模与控制（一） - 基础概念和约定
人形机器人，也被称为腿式机器人，相比于轮式机器人在崎岖地形上具有明显的优势。然而，这种机器人的优势也带来了复杂性的显著增加。虽然现在已经对如何使腿式机器人动态地行走和跑步有了深入的理解，但为了使其在能源、速度、反应性、多功能性和鲁棒性等方面达到更高的水平，仍需要进一步的研究和努力。在这篇博客系列中，将探讨如何对人形机器人进行建模，如何进行其稳定性分析，如何产生和控制其动态运动，以及目前提高其性能的最新趋势。其中，防止机器人跌倒是一个主要的挑战。这一挑战的核心问题是腿式机器人完全依赖于其与地面的接触力。在此背景下，腿部运动的时间性显得至关重要，因为当前的控制策略主要集中在通过模型预测控制（MPC）对未来的运动进行持续预测，或更具体地关注其在极限周期内的轨道稳定性。
以后会涉及的方面 - FK/IK 正/逆运动学 - FD/ID 正/逆运动学 - MPC/NMPC 线性/非线性模型预测控制
以后的专栏中可能会涉及的方面 - RL based control
以强化学习为基础的控制 - RT1& RT2 etc.
1. 空间运动的平移与旋转
人形机器人的运动可以被分解为平移（Translation）和旋转（Rotation）。在这一部分，将详细介绍这两种基本运动的表示方法并且说明在以后的博客中使用的变量命名约定。
平移
平移运动的数学描述为：
- w: 代表参考系 (with respect to)
- a: 起始点或坐标系 (Measured from)
- c: 目标点或坐标系 (Target)
旋转
旋转是空间中点或物体围绕某一轴进行的旋转。例如，我们考虑基坐标系 {b}
的一个基轴的旋转：
这里，
对于确定的系统，我们有9个变量但只有3个自由度的旋转。约束条件如下：
正交性：
右手法则：
综合上述两个条件，我们可以定义三维空间的旋转矩阵为特殊正交群
基于围绕x、y和z轴的旋转，我们可以得到以下的旋转矩阵：
在上述旋转矩阵中，θ代表围绕相应轴的旋转角度。
旋转矩阵与欧拉角 在上文中，我们对旋转矩阵及其与欧拉角的关系进行了展开。欧拉角为我们提供了描述三维空间中物体方向的一种方式，但它们有一个称为“万向节锁”或“奇点”的问题，这意味着在某些特定的角度组合中，它们无法唯一地描述物体的方向。
当在欧拉角表示下，一个物体绕着一个轴旋转到与另一个轴对齐时，我们就不能区分这两个轴的独立旋转了，这种情况就被称为万向节锁。为了避免这个问题，我们可以使用其他的表示方法，例如四元数。
四元数
四元数在描述三维旋转时具有许多优势，它可以避免欧拉角的奇点问题，并且在计算上更加高效和稳定。然而，四元数的直观理解并不容易，它们的形式与我们习惯的笛卡尔坐标或其他常见的空间表示形式不同。
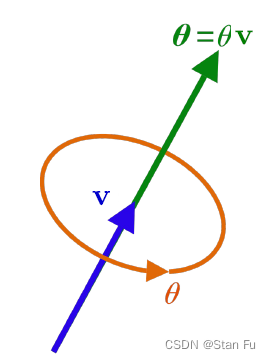
四元数由一个标量部分和一个三维向量部分组成。图中的四元数表示形式为
#### 如何理解四元数？
我们可以通过以下方式理解四元数的旋转：任何3D空间中的旋转都可以等效地看作是围绕一个固定轴的纯旋转。换句话说，给定一个单位长度的向量和一个旋转角度，我们可以使用四元数表示该旋转。这里的向量
最后，值得注意的是，四元数并不是唯一的。对于同一个3D旋转，可能有两个四元数可以表示。这是因为它们可以表示为正旋转和负旋转。
2. 空间代数
变换
在机器人学、计算机图形学和空间信息学中，空间代数主要涉及坐标变换，即如何描述一个点在不同的坐标系中的位置。以下公式描述了这种坐标变换：
这里，
为了方便表示和计算，我们经常使用齐次坐标来描述这种变换：
其中
为了计算变换矩阵的逆，我们可以使用以下公式：
变换的组合表示为：
欧几里得群
对于空间变换，我们有特殊欧几里得群
线速度
线速度描述了点或物体在空间中的移动速度：
角速度
角速度描述了物体在空间中的旋转速度。
其中
第一个等式
定义斜对称矩阵，
表示旋转矩阵的导数
离散积分下的旋转
当我们考虑一个物体在一段很短的时间内的旋转，我们可以使用离散积分来估计这个旋转。给定一个初始旋转
其中，
点的速度
考虑一个点
利用之前的知识，我们可以进一步简化为：
其中，
或者，
速度旋量 Twist
Twist 是用于描述刚体的线性和角速度的一种数学表示。在机器人学和计算机图形学中，它常常用于表示刚体或坐标系的速度。
在上面的公式中，我们有一个6维向量
为了更具体，我们可以将
在这里：
分别代表沿 x、y 和 z 轴的线性速度。 分别代表绕 x、y 和 z 轴的角速度。
这种表示方法提供了一个统一的方法来描述刚体的速度，无论它是进行平移、旋转还是两者的组合。
力
力是一个三维向量，表示为：
扭矩/力矩 Couple/Torque/Moment
力矩或扭矩表示作用在物体上的旋转效应。它可以通过以下公式计算：
其中，
这里，
4. 坐标变换（速度）
在多体动力学和机器人学中，我们经常需要描述或变换物体的速度和位置。这在控制器设计、路径规划和动画模拟中都是至关重要的。坐标变换为我们提供了一个框架，以统一的方式描述这些关系。
速度的坐标变换
考虑两个物体，标记为1和2。物体2相对于物体1可能有其自己的速度，但如果我们想知道物体2相对于一个全局参考系（在此标记为0）的速度，我们需要使用以下公式：
其中：
是物体1相对于全局参考系的速度。 是从物体1到全局参考系的旋转矩阵。 是物体1相对于全局参考系的角速度。
这个公式考虑了物体1的速度、物体2相对于物体1的速度，以及由于物体1的旋转导致的附加速度。
位置的坐标变换
对于物体2的位置，我们有：
这个公式是直观的，表示物体2的位置是由物体1的位置和物体2相对于物体1的位置的组合得到的。
角速度的坐标变换
同样，物体2的角速度可以通过以下方式得到：
这表示物体2的角速度是物体1的角速度和物体2相对于物体1的角速度的组合。
5. 坐标变换（力矩）
在机械工程、机器人学和多体动力学中，我们经常遇到需要描述或变换力和力矩的情况。为了描述这两者，我们使用了一个统一的数学工具：Wrench。
动力旋量 Wrench
Wrench 是一个六维向量，用于描述刚体上的力和力矩。它的定义如下：
其中，
力和力矩的坐标变换
当我们需要从一个坐标系转换到另一个坐标系时，我们可以使用下面的公式：
对于力的转换：
此公式表示，在坐标系1中的力 是由坐标系2中的力 通过旋转矩阵 转换得到的。 对于力矩的转换：
这个公式表示，在坐标系1中的力矩 是由坐标系2中的力矩 和由于力 在坐标系2中相对于坐标系1中的位置 所产生的附加力矩转换得到的。
6. Plücker 符号法
Plücker 符号法是一种在空间运动学和动力学中表示向量的方法。这种表示法有助于简化变换和其他操作。
向量空间
空间运动向量
一个空间运动向量可以表示为：
空间力向量
空间力向量可以表示为：
变换
变换可以用于描述向量如何从一个坐标系转移到另一个坐标系。我们可以有以下定义：
对于空间运动向量:
功率
功率是一个标量，不与任何坐标框架相关。它可以计算为：
加速度 (Acceleration)
在动力学中，物体的加速度是其速度随时间的变化率。在三维空间中，加速度是一个向量，通常表示为
考虑上图中的物体，我们可以有以下描述：
对于物体的角加速度
和线加速度 ： 考虑到坐标系 A，物体的加速度可以进一步细化为：
对于力向量，我们有：
综合以上，我们可以得到加速度的总表达式为：
动量 (Momentum)
动量是物体的质量和速度的乘积，表示物体的运动状态。对于一个刚体：
线性动量：
这里， 是物体的质量，而 是物体质心的速度。 角动量：
其中， 是物体相对于其质心的惯性矩阵，而 是物体的角速度。 空间动量 是线性和角动量的组合：
惯性 (Inertia)
惯性描述了物体对其状态改变的抵抗。对于刚体：
空间惯性 是表示线性和角惯性的6x6矩阵：
坐标系变换 描述了如何在不同的坐标系之间转换惯性：
其中，
- Title: 人形机器人建模与控制（一） - 基础概念和约定
- Author: xiangyu fu
- Created at : 2024-05-06 16:21:47
- Updated at : 2024-06-09 00:13:47
- Link: https://redefine.ohevan.com/2024/05/06/legged_robots/blog-01/
- License: This work is licensed under CC BY-NC-SA 4.0.